
Ez a cikk a Creation Magazin 2021-ben jelent meg.
Hasonló cikkekért rendelj a magazinokból!
Leonhard Euler
A Bibliahívő zseni
Leonhard Euler [ejtsd: ajler] (1707–1783) minden idők egyik legnagyobb és legtermékenyebb matematikusa és elméleti fizikusa volt. Az elméleti és alkalmazott matematika szinte minden területének fejlődéséhez hozzájárult, különösen a számítások, a számelmélet, a jelölésrendszer, a fénytan, az áramlástan, valamint az égi és klasszikus mechanika területén.1
Jelentős eredményeket ért el a térképészet, időszámítás, hajó- és hídépítés valamint a ballisztika területén azáltal, hogy az egyes fizikai kérdéseket matematikai módszerekkel oldotta meg. Vívmányai olyan jelentős tudósok sorába emelik, mint Arkhimédész, Newton és Gauss. A kiváló svájci történész, Emil Fellmann szerint Euler „az emberiség történetének nem csak messze a legtermékenyebb matematikusa, hanem egyik legnagyobb tudósa is volt.”2
Gyermekkora és matematikai tehetsége
Leonhard 1707-ben született a svájci Bázel városában. Apja, aki matematikát tanult, egy református gyülekezet lelkésze volt, amely hangsúlyozta „a keresztény belső újjászületés, a testvéri szeretet és élő hit” fontosságát.3 Mindezeket Leonhard maga is meggyőződéssel vallotta, és soha nem ingott meg hitében.
A fiatal Leonhardot először otthon, az édesapja tanította a matematika alapjaira. 1720-ban jelentkezett a Bázeli Egyetemre, hogy lelkésznek tanuljon. Itt a család egyik barátja, Johann Bernoulli oktatott matematikát, aki később Európa egyik legkiválóbb matematikusa lett. Bernoullit annyira lenyűgözte Leonhard kivételes tehetsége és lelkesedése a téma iránt, hogy szombat délutánonként magánórákat adott neki matematikából, csillagászatból és fizikából, ráadásul Leonard apját is meggyőzte arról, hogy a fiú nem teológiai, hanem matematikusi pályára rendeltetett.
Versenyben a Párizsi-díjért
1727-ben Euler beküldött egy esszét a Francia Tudományos Akadémia által évente meghirdetett Párizsi-díj nevű versenyre, ami abban az időben Európában a legrangosabb tudományos kitüntetéssel járt együtt. Értekezésében azt vizsgálta, hogy a vitorlás hajók árbocainak száma, helyzete és magassága szempontjából mi az az optimális elrendezés, amely mellett maximális sebességet lehet elérni. Munkájáért különdíjban részesült. A későbbi években két újabb különdíjat kapott, és azon további 12 alkalommal, amikor adott be pályaművet, vagy megnyerte a díjat, vagy megosztott díjat kapott.
Oroszországban
Nincs olyan tudományterület, a matematikát is beleértve, ahol ne lehetne megfogalmazni ellentmondásokat. Mégsem kérdőjelezi meg senki a matematika megbízhatóságát.
1727 és 1741 között Euler a Szentpétervári Tudományos Akadémián oktatott, ahol 1731-ben a fizika professzora lett, két évvel később pedig a matematika tanszék vezetőjévé választották. Életrajzírója, Ronald Calinger szerint kutatása széleskörű volt, a következőkkel foglalkozott: „algebra, számtan, csillagászat, ballisztika, kúpszeletek, differenciálgeometria, rugalmasságtan, végtelen sorozatok, zeneelmélet, számelmélet és oszcilláló sorozatok, de fő területe a racionális mechanika volt. Euler meg volt győződve a matematikai tudományok egységéről, ezért minden ág tökéletesítésére törekedett.”4
Gyakorlati problémák megoldásában is részt vett: tűzoltóautókat tervezett, tanácsokkal látta el az orosz haditengerészetet, tankönyveket írt orosz iskolák számára, továbbá egy kétkötetes elemi számtankönyvet is írt németül. Ezen kívül az Orosz Birodalom első pontos, nagyléptékű térképének előkészítésében is segédkezett. Az 1745-ben Orosz atlasz címmel megjelent mű elkészítéséhez a szélességi és hosszúsági fokok pontos kijelölésére volt szükség.
Házasság és család
1734-ban Euler feleségül vette Katharina Gsellt. 13 gyermekük született, akik közül sajnos csak öt érte meg a kisgyermekkort, és csak három élte túl szüleit. Calinger így ír:
Minden este, vacsora után Euler összegyűjtötte gyermekeit, szolgálóit és a házuknál elszállásolt diákokat, és házi áhítatot tartott, ahol felolvastak a Bibliából, és időnként közösen beszélgettek róla. Lefekvés előtt is gyakran olvasott fel gyermekeinek igeverseket vagy bibliai történeteket.5
A Basel-probléma megoldása
1735-ben Euler megoldott egy 1644-ben megfogalmazott matematikai feladványt, amit a világ legnagyobb matematikusai sem tudtak megfejteni, és ezzel egy csapásra világhírűvé vált. A feladvány lényege, hogy meg kell határozni – bizonyítással együtt – a természetes számok négyzetei reciprokának összegét, azaz a következő végtelen sor pontos összegét:

Euler bebizonyította, hogy a sor összege az n növekedésével π2/6-hoz tart. A matematikában jártas olvasók a teljes megoldást elolvashatják a Wikipédián a Basel-probléma címszó alatt.6
A „königsbergi hét híd” problémája
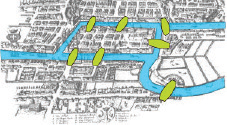
A königsbergi hidak térképe Euler idejében
Kelet-Poroszország egykori fővárosa, Königsberg (mai nevén Kalinyingrád), ma Oroszországban van. A város akkoriban négy szárazföldre oszlott, amelyeket a Prégel folyó hét hídja kötött össze egymással:
A város lakói szabadidejüket azzal töltötték, hogy megpróbáltak egyetlen séta során mind a négy területre eljutni úgy, hogy minden hídon pontosan egyszer haladnak át.
Noha ez senkinek sem sikerült, úgy tűnik, senki sem tudta bebizonyítani, hogy ez lehetetlen. Itt jön képbe Euler! 1735-ben logika (és egy csipetnyi számtan) segítségével megoldotta a problémát. A következő megfigyeléseket tette:

A königsbergi hét híd problémájának modern, grafikus ábrázolása
- Az, hogy a szárazföldi területeken belül merre megyünk, lényegtelen.
- Minden terület esetében két különböző hídon kell átmennünk: az egyiken befelé, a másikon kifelé.
- Ezért minden területre páros számú hídnak kell vezetnie.
- Viszont az egyik területre öt híd vezet, három másikra pedig egyenként három.
- Ezért lehetetlen a fenti feltételek mellett bejárni az összes területet.
Euler ezzel a megoldással a modern gráfelmélet alapjait vetette meg, és előrevetítette a topológia koncepcióját.
1738-ban a jobb szemén egy tályog keletkezett, majd a látását is elveszítette. Ennek komoly következményei lettek a későbbiekben.
Berlini karrier
Mivel Euler a természettudomány és filozófia egyik legnagyobb „sztárja” volt, 1741-ben felkérést kapott egy állás betöltésére Berlinben, a Királyi Porosz Tudományegyetemen. El is fogadta, és az ott töltött 25 év alatt körülbelül 380 cikket írt a matematika különböző alkalmazásairól. Azt a két könyvét is itt írta, amelyek a legnagyobb hírnevet szerezték számára. Egyik a függvényekről szóló Introductio in analysin infinitorum című, 1748-ban megjelent kétkötetes könyve, amely az újkori történelem talán legjelentősebb matematikai tankönyve. A másik pedig a differenciálszámításról szóló Institutiones calculi differentialis című tanulmánya, amelyet 1755-ben adtak ki.
A berlini évek alatt jelent meg a harmadik legjelentősebb könyve is, 1749-ben, a kétkötetes Scientia navalis című műve, amely arról szólt, hogy hogyan lehet maximális stabilitású, vezérlésű és sebességű hajót tervezni – a gyakorlatban ezen tulajdonságok sokszor egymás ellen hatnak.
Bernoulli dicsérete
Newton visszavonulása és Leibniz 1716-ban bekövetkezett halála után a korábban említett, Eulernél 40 évvel idősebb Johann Bernoullit a „matematika hercegeként” tartották számon. Bernoulli korán felismerte egykori tanítványa tehetségét. Eulernek címzett üdvözlő levelei rövidesen minden hízelgés nélküli, mégis őszinte elismerést tükröztek. 1745-ben ezekkel a szavakkal szólítja meg fiatalabb társát: „a páratlan Leonhard Eulernek, a matematikusok hercegének”.7
Úttörés a tudomány népszerűsítésében
1759-ben Eulert felkérték a 14 éves Friederike Charlotte Leopoldine Louise tanítására, aki II. Frigyes porosz király másod-unokatestvére volt. Később Porosz Hercegnő néven vált ismertté.
E célból a következő két év alatt több mint 234 levelet írt neki Euler, amiben tisztán és érthetően, egyszerű szavakkal magyarázott, képletek és formulák használata nélkül. Ezeket a leveleket először a Szentpétervári Akadémia jelentette meg Euler levelei egy német hercegnőnek különböző fizikai és filozófiai témákról címmel (az első két kötetet 1768-ban, a harmadikat pedig 1772-ben).
A második, francia nyelvű kiadásra Párizsban került sor 1787 és 1789 között, Euler halála után. A művet Voltaire tanítványa, Nicolas de Condorcet szerkesztette, aki kifogásolta Euler Istenre ill. Ádámra és Évára vonatkozó utalásait (amelyek arról tanúskodtak, hogy Euler Mózes első könyvét, más néven a Teremtés könyvét hiteles történelemkönyvnek tartotta), ezért egy részüket szándékosan kihagyta. Az angol szerkesztő, Henry Hunter, a kihagyott utalások nagy részét szándékosan visszavette az 1795-ben Levelek címmel megjelent angol fordításába.
Calinger a Leveleket „a 18. század legalaposabb és legnagyobb tekintéllyel bíró, tudományt népszerűsítő művének”8 nevezte. Az érintett témakörök között szerepel például a gravitáció; az árapályjelenség; a naprendszer; Newton törvényei; a hang, fény, elektromosság és mágnesesség természete; a légkör; a hideg és a meleg; az ágyúgolyó pályája; és még igen sok más. Elmagyarázta, hogyan működnek különböző tudományos eszközök, mint pl. a hőmérő, távcső, mikroszkóp; hogyan épül fel a szem; hogyan működik a látás; stb. Emellett szillogisztikus diagramok segítségével logikát is tanított a hercegnőnek (ld. a következő oldalon: Logikát fejlesztő Euler-diagramok).
Euler több levelében is megosztotta a hercegnővel gondolatait Istenről, az imádságról, az örök életről, gonoszról és bűnről, az isteni igazságosságról, a szenvedés hasznáról, és a bűnösök megtéréséről. A 41. levélben, a szem csodájának magyarázatánál ezt írta:
Noha még nagyon messze vagyunk attól, hogy [a szem működését] tökéletesen megértsük, mindaz a kevés, amit tudunk, bőven elég arra, hogy meggyőződjünk a Teremtő hatalmáról és bölcsességéről. A szem szerkezetében olyan tökélyt fedezhetünk fel, amelyet még a legnagyobb géniusz sem tudna elképzelni.9
Friederike hercegnő, aki minden bizonnyal a világ legműveltebb tinédzsere volt, szorgalmazta a levelek kiadását, hogy sokak számára elérhetőek legyenek.
A mű 1800-ra már harminc kiadást élt meg, és nyolc nyelvre fordították le.
Aktív hitvédő
Euler abban az időszakban élt, amit tévesen „felvilágosodás” korának neveznek. Amikor olyan szkeptikus filozófusok, mint Voltaire (1694-1778), Hume (1711-1776), Kant (1724-1804), és „szabadgondolkodású” társaik megvetéssel tekintettek a Biblia Istenére, megtagadták a keresztény hitet, és azt állították, hogy az emberiség kizárólag az értelem segítségével tud fejlődni. Mindezek ellenére Euler állhatatosan kitartott keresztény hite mellett, és 1746-ban A kinyilatkoztatás [ti. a Biblia] védelme a szabadgondolkodók ellenvetéseivel szemben című szenvedélyes levélben válaszolt kora szkepticizmusára. Formailag ez egy röpirat volt, ami 53 számozott bekezdésből állt.
A levél elején arról beszél, hogy a boldogság magába foglalja az igazság megértését, mivel Isten az igazság, és a világ az Ő hatalma és bölcsessége által keletkezett. Kiáll amellett, hogy Isten minden igazság forrása, és Ő maga a végső jó. Isten az ember szívébe írta a természetes törvényt, és azt várja el, hogy cselekedeteinket ahhoz igazítsuk. Mivel a törvény magától Istentől ered, az ennek való engedetlenség lázadás a mindenható Isten ellen, ezért isteni ítéletet von maga után.
Euler szerint a Biblia olyan módon mutatja be minden emberi kötelesség egyetlen és valódi forrását, ami egyetlen bibliai író tehetségével sem magyarázható, ezért úgy tekintünk a Bibliára, hogy az Istentől származik. Számtalan hívő nemcsak látta Krisztust a feltámadása után, hanem beszélt is vele, vagyis nem csak a képzeletük játszott velük. Jézus Krisztus feltámadása tehát cáfolhatatlan tény, kizárólag Isten munkája, és ezért hittel elfogadhatjuk az evangéliumokban található, evilágra és a túlvilágra vonatkozó ígéreteket.
A szabadgondolkodókkal kapcsolatban Euler kijelentette, hogy egyetlen ellenérvet sem tudnak felhozni a Szentírás isteni ihletettségét igazoló érvekkel szemben. A Biblia valóban tartalmaz olyan dolgokat, amikkel a szabadgondolkodók nem értenek egyet – ha nem így lenne, az a Bibliára nézve ártalmas lenne. A Bibliában található látszólagos ellentmondásokkal kapcsolatban kifejtette, hogy nincs olyan tudományterület (a matematikát is beleértve), ahol ne lehetne megfogalmazni hasonló vagy még erősebb kritikákat vagy ellentmondásokat. Mégsem kérdőjelezi meg senki a matematika megbízhatóságát. A szabadgondolkodók kifogásait már régen megcáfolták, de mivel nem az igazság vágya hajtja őket, nem fogadják el a cáfolatokat, és újból és újból előhozakodnak gyenge és abszurd érveikkel, mondta Euler.
Vissza Szentpétervárra
1766-ban Euler a Birodalmi Akadémia ajánlatát elfogadva visszatért Szentpétervárra. Néhány hónappal később súlyosan belázasodott, és az ép (bal) szemében fellépő problémák miatt a látása jelentősen sérült. Calinger ezt írja:
Ragyogó memóriája, gazdag képzelőereje, állhatatossága, csillapíthatatlan kíváncsisága, és tudományos érzéke még a vakság előszobájában sem hagyta el. A kutatás iránti szenvedélye, valamint a legnehezebb problémák megoldásával járó öröm miatt látásának elvesztésével kapcsolatban magabiztosan így nyilatkozott: „még egy zavaró tényező elhárítva”.10
Bámulatos memóriáját jól példázza az, hogy Vergilius Aeneis című teljes művét fejből tudta, sőt még azt is, hogy az egyes oldalakon melyik volt az első, illetve az utolsó sor.11
Rendkívül termékeny írói tevékenységét még egyre romló látása sem vetette vissza, sőt, valójában még nagyobb lendületet adott neki! „Cikkek és könyvek özönét írta. Összesen 415 esetben vagy ő maga volt a szerző, vagy a nyomtatásig való eljutás folyamatában volt aktív szerepe. Ezek közül több mint 150 csak halála után jelent meg.” 12
Ebben az időszakban írta másik nagysikerű művét: a sokat dicsért, 500 oldalas Átfogó útmutató az algebrához (Complete Guide to Algebra) című könyvét. 1773 áprilisában befejezte élete utolsó nagyobb, navigációról szóló, egyszerűsített tanulmányát, amelynek címe A hajóépítés és irányítás átfogó elmélete minden navigációban érintett számára. A könyv minden olyan hajómozgásformát taglal, amely a tengerészek szempontjából nélkülözhetetlen, mégpedig olyan nyelvezetet használva, hogy matrózok, tengerészek, árbockészítők és hajóépítők is könnyen megértsék.
1783-ban halt meg, stroke szövődményei következtében.
Logikát fejlesztő Euler-diagramok
Euler egyik kevésbé ismert újítása azon diagramok voltak, amik segítségével Friederike hercegnőnek tanított logikát. Először a 103. levelében használta a 398. oldalon, és különböző feltevésekre alkalmazta egészen a 108. levélig. A tudósról elnevezett Euler-diagramokat a Venn-diagramokkal együtt 1960 óta használják különböző halmazelemek egymáshoz való viszonyának szemléltetésére (a John Venn tudós által 1880-as években bevezetett Venn-diagramok olyan speciális Euler-diagramok, amelyek egymással átfedésben vannak). Az újítás jelentősége nem az alakzatok méretében vagy formájában, hanem az átfedésük módjában rejlik. Az az alakzat, amely teljes mértékben egy másikban helyezkedik el,
részhalmazt jelöl.
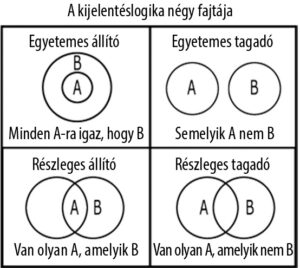
Euler diagramja Friederike hercegnőnek írt 103. leveléből, amellyel logikát tanított neki.
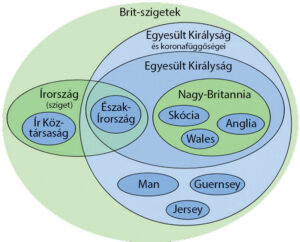
A Brit-szigetek Euler-diagramja (Wikipédia)
Emlékezés és tisztelgés
Calinger így írt Euler halálhíre kapcsán:

Euler-emléktábla Riehenben, amit 1960-ban, a Bázeli Egyetem 500. évfordulója alkalmából állítottak. A név és az évszámok alatt a következő olvasható: „Matematikus, fizikus, mérnök, csillagász és filozófus. Fiatalkorát Riehenben töltötte. Nagyszerű tudós és jólelkű ember volt.”
A tudományos világ egyetért abban, hogy egyik legnagyszerűbb munkatársát veszítette el. Mélységes részvétét fejezi ki a négy fő királyi tudományos akadémia: Londonban, Párizsban, Berlinben és Szentpéterváron; valamint számtalan egyesület Bázelben, Lisszabonban, Münchenben, Stockholmban és Torinóban, amelyeknek Euler tagja volt.13
Halála után hátrahagyott kiadatlan írásai a Szentpétervári Akadémia számára csaknem 50 évre elegendő további kiadni való anyagot jelentettek.
Opera Omnia (Összes művei) c. munkáját a Svájci Tudományos Akadémia 1911 óta jelenteti meg. E cikk megjelenéséig (2017) összesen 72 kvartó kiadás látott napvilágot, három sorozatban: a, matematika; b, mechanika és csillagászat; illetve c, egyéb témákban; körülbelül 35000 oldalnyi anyag. A negyedik sorozat jelenleg feldolgozás alatt áll: Euler 275 különböző személynek írt 3300 francia, latin, német, orosz és (néhány) angol nyelvű levelét tartalmazza 10 kötetben.
Arcképe számos svájci, orosz, német és egyéb bélyegen, továbbá a svájci 10 frankos bankjegyen is megjelent. A csillagászok Euler iránti tiszteletből a hold egyik kráterét, illetve egy üstököst is elneveztek róla.
Szelídsége és egyszerű élete ellenére korának legnagyobb matematikusa volt. Élete végén tanítójaként tekintett rá Európa minden matematikusa, és ez a 19. illetve 20. században sem változott. Például a kiváló francia (ateista) matematikus, Pierre Simon Laplace (1749-1827) ezt mondta: “Olvassátok Eulert! Olvassátok Eulert! Ő mindannyiunk mestere!”14 Ez az Euler pedig elkötelezett, istenfélő, bibliahívő keresztény volt.
Amit Eulernek köszönhetünk
Számos ma használt matematikai jelölést és fogalmat Euler alkotott, népszerűsített vagy egységesített, mint például:
- f(x) a függvények,
- x, y, és z az ismeretlenek,
- a, b, c a háromszög oldalai,
- A, B, C a szemközti csúcsok,
- R és r a háromszög körülírt és beírt köre sugarának jelölésére.
- A trigonometrikus függvények rövidítései: sin, cos, tan, csc, sec, és cot.
- A π széleskörű használata (noha a szimbólumot nem ő vezette be).
- ∑ az összegzés,
- Δ a véges differencia,
- i a képzetes egység √-1
- e a természetes logaritmus alapja, e ≈ 2,71828.
- Euler képlete a rúd kritikus törőerejére: Pcr = π2EI/(KL)2
- A neki tulajdonított eiπ = –1 ún. Euler-képletet (vagy másképpen eiπ + 1 = 0) a matematikusok ‘az egyik leggyönyörűbb matematikai képletként’ tartják számon, mert (számukra) nagyon sokatmondó, mivel az öt legfontosabb matematikai állandót egyetlen képletben foglalja magában.
- Euler soklapú testekre vonatkozó ún. poliédertétele: V – E + F = 2 (ahol V = a csúcsok száma, E = az élek száma, és F = az egyszerű (azaz lyukakat nem tartalmazó) háromdimenziós konvex poliéder lapjainak száma).
Egy megdöbbentő lista, hogy milyen sok mindent neveztek el Eulerről (angolul): en.wikipedia.org/wiki/List_of_things_named_after_Leonhard_Euler
Hivatkozások és megjegyzések
1. Lásd Ronald S. Calinger részletes életrajzát: Leonard Euler: Mathematical Genius in the Enlightenment, Princeton University Press, USA, 2016, amely a cikk legfőbb forrása.
2. Fellmann, Emil A., Leonhard Euler (in German), Rowohlt Taschenbuch Verlag, Reinbek bei Hamburg, Germany, p.9. Fellmann (1927-), aki matematikából, fizikából és filozófiából is tudományos háttérrel rendelkezik, számos európai – köztük a Bonni – egyetemen tanított vendégprofesszorként.
3. Calinger, Ref. 1, p. 11.
4. Calinger, Ref. 1, p. 92.
5. Calinger, Ref. 1, p. 188.
6. Később egy precízebb bizonyítást is közölt, ami más matematikusok észrevételével együtt elérhető: https://en.wikipedia.org/wiki/Basel_problem
7. Fellman, ref. 2, p. 24.
8. Calinger, Ref. 1, p. 465.
9. Letters of Euler to a German Princess, trans. by Henry Hunter, Vol. 1, No. 41, p. 165, 1802.
10. Calinger, Ref. 1, p. 454.
11. Az Aeneis egy 9896 hexameterből álló latin költemény, amit Vergilius Kr. e. 29 és 19 között írt.
12. Calinger, Ref. 1, p. 456.
13. Calinger, Ref. 1, p. 532.
14. Journal des Savants, January 1846, p. 51.
Fordította: Ficsor Donát
Lektorálták: Sebestyénné Preska Ágnes és Királyné Lilla




